전에 알아본 k-means 기법은 극도로 큰 값(혹은 작은 값)이 데이터의 분포를 사실상 왜곡할 수 있기 때문에 이상치에 민감하다.
이를 위해 군집에서 객체들의 평균값을 취하는 대신에 군집에서 가장 중심에 위치한 객체인 medoid를 사용할 수 있다.
k-medoids 군집화 알고리즘의 기초적인 방법은 각 군집에서 대표 객체(medoids)를 임의로 찾음으로써 n개의 객체 중에서 k개의 군집을 찾는 것이다.
남은 각각의 객체는 가장 비슷한 medoids에 군집된다.
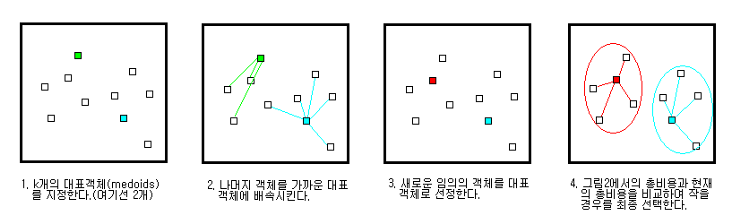
Step 1. n개의 객체 중 대표 객체(medoids)를 k개 지정한다. (n>k)
Step 2. k개의 medoids를 지정 후, 나머지 객체를 유사성이 가장 높은 medoid에 배속한다. 여기서 유사성은 거리측도를 활용한다.
Step 3. medoid가 아닌 다른 객체를 임의로 지정한다.
Step 4. 본래의 medoid와 임의의 medoid간의 총 비용(cost)를 계산한다.(cost는 거리측도의 값을 모두 더한 것을 사용한다.)
Step 5. 만약 총 비용이 음수인 경우, 임의의 medoid를 기존의 medoid와 교체한다.
Step 6. 변화가 없을 때까지 Step2~Step5를 반복한다.
위의 과정을 알고리즘으로 짜기 위해 더 쉽게 생각해보자.
1) n개의 데이터 중 k개의 대표 객체를 선택할 수 있는 모든 경우를 생각한다. (n Combination k 개의 경우)
2) i번째 경우에서의 총 비용은 k개의 군집을 형성한 후 군집의 배속된 객체와 군집 중심과의 거리를 모두 더한 것이 된다.
3) 이러한 총 비용을 모든 경우의 수에서 비교하여 가장 작은 경우일때의 대표 객체와 군집을 최종적으로 선택한다.
알아본 것과 같이 k-medoids 알고리즘은 k-means에 비해 이상치에 덜 영향을 받게 되지만, 군집의 수와 데이터의 총 수에 비례하여 고비용으로 처리되게 된다. 따라서 두 가지의 알고리즘을 선택하는 것은 이상치의 유무와 저용량의 데이터를 기준으로 삼아얄 것이다.
출처 : http://blog.naver.com/asus1984?Redirect=Log&logNo=120065317344
'Fundamental > Technical ' 카테고리의 다른 글
| 802.1Q (VLAN) (0) | 2014.07.31 |
|---|---|
| Kohonen Network 기법(코호넨 네트워크) (데이터마이닝) (0) | 2014.05.12 |
| k-means 기법 (데이터마이닝) (0) | 2014.05.12 |
| Data Clustering (0) | 2014.05.12 |
| Network 용어정리 (0) | 2014.04.22 |
댓글