k-means 기법 (데이터마이닝)

k-means 알고리즘은 n개의 객체들의 집합을 k개의 군집으로 분해한다. 군집 유사성은 군집에서 군집의 무게중심으로 볼 수 있는 객체들의 평균값을 측정한다. k-means 알고리즘이 진행되는 과정은 아래의 그림과 같다.

 

 

 

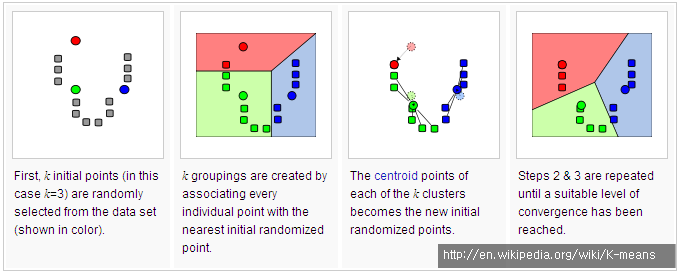
Step 1. 군집 수 k를 결정하고, 각 군집에 초기치 또는 군집 중심을 1개씩 할당한다.

 

Step 2. 모든 데이터를 가장 가까운 군집 중심에 배속시킨다. (유클리드 거리를 이용)

 

Step 3. 각 군집에 배속된 데이터와 새로운 군집 중심사이의 거리가 최소가 되도록 새로운 군집 중심을 계산한다.

 

Step 4. 군집 중심이 변화가 거의 없을 때까지 Step2와 Step3을 반복한다.

 

 

R에 있는 iris 데이터를 활용하여 알고리즘을 직접 짜보았다.

### 군집중심으로 최소거리에 해당하는 군집에 데이터를 배속 ### grouping<-function(centroid,data,k,n,r){      data<-data[,-r]      dist<-matrix(0,k)      group<-matrix(0,n)      for(i in 1:n){           for(j in 1:k){                dist[j]<-dist(rbind(centroid[j,],data[i,]))           }           min_value <- min(dist)           for(z in 1:k){                if(min_value == dist[z]){ group[i]<-z }           }      }      data[,r]<-group      data } ### 새로운 군집 중심을 계산 ### new_centroid<-function(centroid,data,k){      last<-length(data)      for(i in 1:k){           aa<-which(data[,last] == i)           centroid[i,]<-mean(data[aa,-last])      }      centroid } ### 전체적인 함수 실행부분 ### k_means<-function(data, k){      r<-ncol(data)                                               ## Dimensional      n<-nrow(data)                                              ## Number of data      samp<-sample(n,k)            centroid<-data[samp,]                                   ## initial centroid          data <- grouping(centroid,data,k,n,r+1)      n_centroid<-new_centroid(centroid,data,k)      while(identical(centroid, n_centroid)==FALSE){           centroid<-n_centroid           data<-grouping(centroid,data,k,n,r+1)           n_centroid<-new_centroid(centroid,data,k)      }      print(n_centroid) } ### 함수 실행 ### data<-iris[,-5] k_means(data,3)

 

 

위의 결과를 가지고 R에서 제공하는 kmeans()함수와 클레멘타인에서 제공하는 k-means의 3가지 결과를 비교하였다.

 

직접 작성한 코드의 결과

Sepal.Length  Sepal.Width   Petal.Length   Petal.Width 6.850000         3.073684       5.742105         2.071053 5.901613         2.748387       4.393548         1.433871 5.006000         3.428000       1.462000         0.246000

 

 

R의 kmeans() 결과

Sepal.Length  Sepal.Width   Petal.Length   Petal.Width 6.850000        3.073684        5.742105        2.071053 5.901613        2.748387        4.393548        1.433871 5.006000        3.428000        1.462000        0.246000

 

 

클레멘타인의 결과

Sepal.Length  Sepal.Width   Petal.Length   Petal.Width 6.846                3.082              5.703                2.079 5.889                2.738              4.397                1.418 5.006                3.428              1.462                0.246

 

 

군집이 3개일때의 군집들의 평균벡터는 위와 같다. R과 클레멘타인에서의 결과가 표준오차범위에서 일치하다.(이는 클레멘타인의 결과를 확인)

군집의 수가 많아짐에 따라 각 결과마다에 차이들이 나타나지만 큰 차이를 보이고 있지는 않는다.

 

 

 

 

 

출처 : http://blog.naver.com/asus1984?Redirect=Log&logNo=120065317344